El estándar IEEE 754 ha sido definido por el Instituto de Ingenieros Eléctricos y Electrónicos (Institute of Electrical and Electronics Engineers, IEEE) y establece dos formatos básicos para representar a los números reales en la computadora digital: precisión simple y precisión doble.

Precisión Simple en el Estándar IEEE 754

En precisión simple, para escribir un número real se usan 32 bits (4 bytes): 1 bit para el signo (s) del número, 23 bits para la mantisa (m) y 8 bits para el exponente (exp), que se distribuyen de la siguiente forma:

Figura - Representación de un número real con precisión simple en el estándar IEEE 754.

El exponente se suele representar en Exceso a 2^n-1-1, mientras que, para la mantisa, normalmente se utiliza Signo Magnitud. Además, la mantisa se suele normalizar colocando la coma decimal a la derecha del bit más significativo.

Ejemplo 1: Para escribir el número 101110,010101110100001111100001111100010011₂ en el estándar IEEE 754 con precisión simple, exponente en Exceso a 2^n-1-1 y mantisa en Signo Magnitud, primero hay que normalizarlo:

1,01110010101110100001111100001111100010011₂ x 2⁵

El exponente, en Exceso a 2^n-1-1, será:

5₁₀ + (2^8-1 - 1)₁₀ = 5₁₀ + (27 - 1)₁₀ = 5₁₀ + (128 - 1)₁₀ = 132₁₀ = 10000100_{EX.
a 127}

De la mantisa se cogen los bits 23 bits más significativos:

1,0111001010111010000111

El resto de bits no se pueden representar, ya que, no caben en la mantisa. Sin embargo, cuando la mantisa se normaliza situando la coma decimal a la derecha del bit más significativo, dicho bit siempre vale 1. Por tanto, se puede prescindir de él, y coger en su lugar un bit más de la mantisa. De esta forma, la precisión del número representado es mayor. Así, los bits de la mantisa serán:

01110010101110100001111

Al bit omitido se le llama bit implícito. Por otra parte, el bit de signo vale 0, ya que, el número es positivo. En consecuencia, el número se puede representar como:

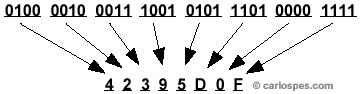
Los programadores, para representar a los números reales en este formato, suelen utilizar el Sistema Hexadecimal.

Ejemplo de pasar del Sistema Binario al Hexadecimal

Así pues,

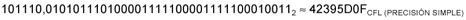En este caso, los números no son exactamente iguales, ya que, con precisión simple no se han podido representar todos los bits de la mantisa.

Ejemplo 2: Dado el número 3E400000_CFL del estándar IEEE 754 con precisión simple, exponente en Exceso a 2^n-1-1 y mantisa en Signo Magnitud con bit implícito, para averiguar a qué número representa en base 10, se pueden realizar los siguientes pasos:

1º) Convertir 3E400000₁₆ a base 2:

2º) Obtener los bits del signo, de la mantisa y del exponente:

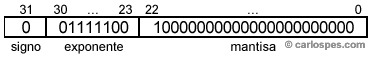3º) Pasar el exponente a base 10:

01111100₂ - (2^8-1 - 1)₁₀ = 124₁₀ - (2⁷ - 1)₁₀ = 124₁₀ - (128 - 1)₁₀ = 124₁₀ - 127₁₀ = -3

4º) Escribir el número en notación científica. Para ello, la mantisa se debe escribir con el bit implícito (1), seguido de la coma decimal (,) y de los bits de la mantisa (10000000000000000000000), teniendo en cuenta que los ceros por la derecha se pueden despreciar. Por otra parte, el número es positivo, ya que, el bit de signo es 0. Por tanto, el número es:

1,1 x 2^-3

5º) Expresar el número en base 10. Para ello, hay dos formas de hacerlo, la primera es:

1,1 x 2^-3 = 0,0011₂ = ( 2^-3 + 2^-4 )₁₀ = 0,125₁₀ + 0,0625₁₀ = 0,1875₁₀

y la segunda:

1,1 x 2^-3 = ( ( 2⁰ + 2^-1) x 2^-3 )₁₀ = ( ( 1 + 0,5) x 0,125 )₁₀ = ( 1,5 x 0,125 )₁₀ = 0,1875₁₀

Por tanto,

3E400000_{CFL
(PRECISIÓN SIMPLE)} = 1,1 x 2^-3 = 0,0011² = 0,1875₁₀

Precisión Doble en el Estándar IEEE 754

Por otro lado, en precisión doble, para escribir un número real se emplean 64 bits (8 bytes): 1 bit para el signo (s) del número, 52 bits para la mantisa (m) y 11 bits para el exponente (exp).

Figura - Representación de un número real con precisión doble en el estándar IEEE 754.

Ejemplo 3: Si se quiere escribir el número 19,5625₁₀ en el estándar IEEE 754 con precisión doble, exponente en Exceso a 2^n-1-1 y mantisa en Signo Magnitud con bit implícito, los pasos a seguir son:

1º) Cambiar 19,5625₁₀ a base 2. Primero la parte entera:

y, a continuación, la parte fraccionaria:

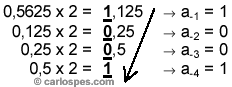De modo que,

19,5625₁₀ = 10011,1001₂

2º) Normalizar el número binario obtenido, colocando la coma decimal a la derecha del bit más significativo:

10011,1001₂ = 1,00111001 x 2⁴

3º) Escribir el exponente en Exceso a 2^n-1-1:

4₁₀ + (2^11-1 - 1)₁₀ = 4₁₀ + (2¹⁰ - 1)₁₀ = 4₁₀ + (1024 - 1)₁₀ = 1027₁₀ = 10000000011_{EX. a 1023}

4º) Establecer la mantisa utilizando bit implícito. Para ello, se cogen los ocho bits que están a la derecha de la coma (00111001) y el resto de la mantisa se rellena con ceros:

0011100100000000000000000000000000000000000000000000

5º) Expresar el número en el estándar IEEE 754 con precisión doble. En este caso, hay que tener en cuenta que el bit de signo vale 0, ya que, el número es positivo:

6º) Representar el número en hexadecimal:

De tal forma que,

19,5625₁₀ = 10011,1001₂ = 1,00111001 x 2⁴ = 4033A00000000000_{CFL(PRECISIÓN
DOBLE)}

Casos especiales en el Estándar IEEE 754

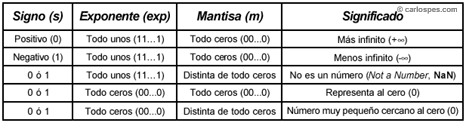
Tanto en precisión doble como en precisión simple, existen algunos casos especiales que dependen de los valores del signo, del exponente y de la mantisa:

Figura - Casos especiales en el estándar IEEE 754 con precisión simple o doble.

Los dos últimos casos merecen especial atención, ya que, cuando todos los bits del exponente son ceros (00...0), esto quiere decir que no se está utilizando bit implícito. Si, además, la mantisa es todo ceros (00...0), el número representado es el cero (0), pero si la mantisa es distinta de todo ceros, el número que se está representando es muy pequeño, de forma que, el exponente valdrá -126 ó -1022, dependiendo de si el número está escrito en precisión simple o doble, respectivamente.

Ejemplo 4: Dado el número 805C0000_CFL del estándar IEEE 754 con precisión simple, exponente en Exceso a 2^n-1-1 y mantisa en Signo Magnitud con bit implícito, para averiguar a qué número representa en base 10, se pueden realizar los siguientes pasos:

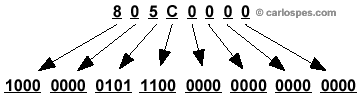
1º) Convertir 805C0000₁₆ a base 2:

2º) Obtener los bits del signo, de la mantisa y del exponente:

3º) Al observar que todos los bits del exponente son ceros (00000000) y la mantisa es distinta de todo ceros, se deduce que es un caso especial. Se está representado a un número muy pequeño sin bit implícito y, por tanto, el exponente es -126.

4º) En notación exponencial, puesto que en este caso no se utiliza bit implícito, la mantisa se escribe con un cero (0), seguido de la coma decimal (,) y de los bits de la mantisa (10111000000000000000000). En cuanto al signo del número, es negativo, ya que, el bit de signo es 1. Con todo ello, el número es:

-0,10111 x 2^-126

5º) Expresar el número en base 10:

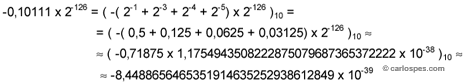¿Cómo calcular el valor en base 10 de un número escrito en IEEE 754?

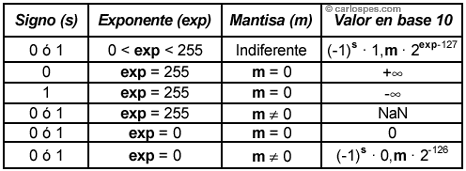
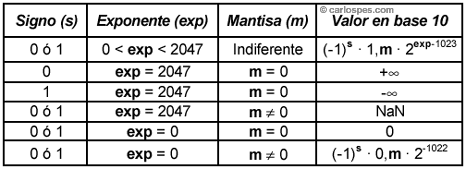
En las dos tablas siguientes se resumen los cálculos que hay que realizar para deducir el valor en base 10 de un número escrito en el estándar IEEE 754 con precisión simple o doble.

Tabla para pasar del estándar IEEE 754 con precisión simple a base 10

Figura - Cálculo del valor en base 10 de un número escrito en IEEE 754 con precisión simple.

Tabla para pasar del estándar IEEE 754 con precisión doble a base 10

Figura - Cálculo del valor en base 10 de un número escrito en IEEE 754 con precisión doble.

Rangos de representación en el Estándar IEEE 754

Los rangos de representación en el estándar IEEE 754 con precisión simple y doble, exponente en Exceso a 2^n-1-1 y mantisa en Signo Magnitud con bit implícito, son los siguientes:

Figura - Rango de representación en el estándar IEEE 754 con precisión simple.

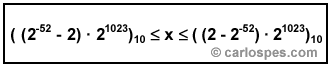Figura - Rango de representación en el estándar IEEE 754 con precisión doble.

Ambos rangos de representación son discontinuos, es decir, no se pueden representar todos los números reales que existen entre dos cualesquiera de ellos. Esto es debido a que entre dos números reales cualesquiera siempre existen infinitos números, sin embargo, sólo se dispone de un número determinado de bits para representar a los números reales. Por esta razón, en las computadoras digitales no se pueden representar a todos los números reales. Por ejemplo, con precisión simple, alrededor del número cero (0) existen infinitos números reales, mayores que -2^-126 y menores que 2^-126, que no son representables. Gráficamente: