|
|
|
|
|
| |
| CarlosPes.com
> Curso
de Representación de los Datos
> Conversión de Base 10 a Base (b) |
| |
Conversión de Base
(b) a Base (c), ambas distintas de 10
|
| |
|
|
|
¿Cómo
pasar de una base a otra?
|
|
Convertir
un número N de base (b)
a otra base (c), ambas distintas de
10, se puede hacer en los dos pasos siguientes:
- Convertir
el número Nb de base
(b) a base 10.
- Convertir
el número N10 de base
10 a base (c).
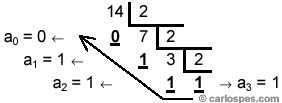
Ejemplo
1: Usando el
método descrito, para convertir el
número 16,518
a base 2, en primer lugar lo pasaremos a base
10 con el Teorema
Fundamental de la Numeración (TFN):
16,518
= 1∙81 + 6∙80 + 5∙8-1
+ 1∙8-2 = 8 + 6 + 0,625 + 0,015625 = 14,64062510
y, a continuación, cambiaremos el número
obtenido, 14,64062510,
a base 2. Los cálculos de la parte
entera son: |
|
 |
|
| y
las operaciones de la parte fraccionaria son: |
|
 |
|
Por
tanto,
16,518
= 14,64062510 = 1110,1010012
Sin embargo, puesto que las bases de los Sistemas Binario y Octal, (2)
y (8), ambas son potencias de 2, es decir,
2 = 21 y 8 = 23, las
conversiones de octal a binario y viceversa se pueden realizar de forma
directa. Para ello, hay que conocer la correspondencia de
dígitos que existe entre ambas bases. |
|
 |
|
| Figura - Tabla de correspondencias
entre los dígitos de los Sistemas Octal y Binario. |
|
| De
la tabla se deduce que, por ejemplo, el número 68
equivale
al 1102, el
número 112
equivale al 38
ó el
número 548
equivale al 1011002,
ya que: |
|
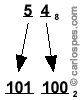 |
|
| En
consecuencia, para convertir el número 16,518
a binario,
podemos hacer corresponder cada uno de sus dígitos con sus
tres equivalentes en binario, de forma que: |
|
 |
|
Los
ceros a la izquierda de la parte entera o a la derecha de la parte
fraccionaria se desprecian. Así pues, obtenemos el resultado
que ya sabíamos,
16,518
= 1110,1010012
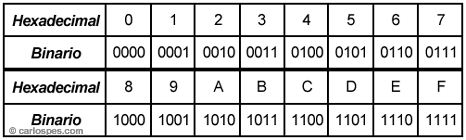
Ejemplo 2: Para convertir al Sistema Hexadecimal
(base 16) el
número 1000000001111,112,
igualmente, se puede usar la tabla
de correspondencias entre los dígitos de los Sistemas
Hexadecimal y Binario, haciendo corresponder grupos de cuatro bits con
los dígitos equivalentes en hexadecimal. |
|
 |
|
| Figura - Tabla de correspondencias
entre los dígitos de los Sistemas Hexadecimal y Binario. |
|
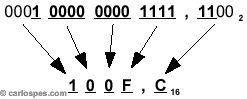
| De
tal manera que: |
|
 |
|
Por
tanto,
1000000001111,112
= 100F,C16
Si primero pasásemos el número a base 10,
haríamos:
1000000001111,112
= 212 + 23 + 22
+ 21 + 20 + 2-1
+ 2-2 =
= 4096 + 8 + 4 + 2 + 1 + 0,5 + 0,25 =
= 4111,7510
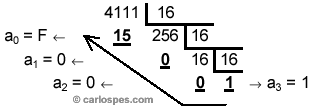
convirtiendo, después, el número 4111,7510
a base
16. Así pues, tendríamos que realizar las
siguientes divisiones para la parte entera: |
|
 |
|
| y
las siguientes multiplicaciones para la parte fraccionaria: |
|
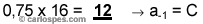 |
|
y
como no podía ser de otra forma,
1000000001111,112 = 4111,7510 = 100F,C16 |
|
|
|
|
|
|
|
|