Los
números escritos en Binario
Puro (BP)
sólo pueden ser positivos, ya que, en este tipo de
representación los números negativos no
están
contemplados. Por tanto, su rango de representación va desde
el
número 010
hasta el número (2n
- 1)10, siendo n el
número de bits
dedicados a representar a los números enteros. De modo que,
en
este sistema de numeración, el rango de valores que puede
tomar
un cierto número x,
viene dado por la expresión:
Figura.
Rango de representación en Binario Puro.
Ejemplo
1: En Binario Puro, para n = 8, el rango de
representación es:
De forma que, se pueden representar 28 = 256
números enteros, que van desde el 010 hasta el 25510.
Ejemplo 2: En
Binario Puro, para n = 8,
el número 2310 se representa de
la siguiente manera:
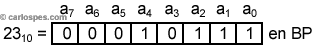Ejemplo
3: En Binario Puro,
para n = 8,
los números -6810 y 37910 no se pueden
escribir, porque están fuera de su rango de
representación (010 <= x <= 25510).
Por otra parte, dado un número (N) en Binario Puro,
para calcular su valor en base 10, se debe utilizar la
fórmula:
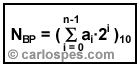Figura. Fórmula
para calcular, en base 10, el valor de un número escrito en
Binario Puro.
Ejemplo
4: Si se quiere calcular el
valor en base 10 del número 10110001BP,
aplicando la fórmula dada, se obtiene que:
10110001BP
= ( 1∙27 + 1∙25 + 1∙24
+ 1∙20 )10 = ( 128 + 32 +
16 + 1 )10 = 17710
Todos los sistemas de representación de números,
ya sean
estos enteros o reales, tienen el inconveniente principal de que al
llevar a cabo operaciones matemáticas con dichos
números,
se puede producir desbordamiento.
El desbordamiento
sucede cuando el resultado de una operación está
fuera del rango de representación.
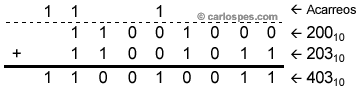
Ejemplo
5: Para n = 8, al calcular
la suma de los números 11001000BP
y 11001011BP,
se producirá desbordamiento:
11001000BP
y 11001011BP
equivalen a 20010
y 20310,
respectivamente. Por tanto, la suma de ambos números
sería 40310,
que está fuera del rango de representación para n = 8 (010 <= x <= 25510).
Obsérvese que, para representar al número 40310 en Binario Puro se
necesitan 9 bits, uno más de los disponibles.
Por otro lado, para saber de antemano el número n de cifras
necesarias para representar en Binario Puro a un determinado
número N
del Sistema Decimal, se puede calcular el logaritmo en base 2 del
número decimal, de forma que:
Ejemplo
6: Si se quiere saber cuantas
cifras se necesitan para representar al número 2710 en Binario Puro,
se debe calcular el logaritmo en base 2 de 2710.
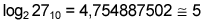Por tanto, se necesitan 5 bits. De hecho, se puede comprobar que,
2710 =
11011BP
|
