3.2 Conversión de base 10 a base (b) - Curso de Representación de los Datos de Carlos Pes

Este tipo de conversión se utiliza para cambiar un número N de base 10 a cualquier otra base (b). Para ello, se deben realizar dos pasos por separado:

Convertir la parte entera del número N₁₀, dividiéndola, sucesivamente, entre b, hasta obtener un cociente más pequeño que b. La parte entera del número que estamos buscando lo compondrá el último cociente y los restos que se hayan ido obteniendo, tomados en orden inverso.
Convertir la parte fraccionaria del número N₁₀, multiplicándola, repetidamente, por b, hasta obtener un cero en la parte fraccionaria o hasta que se considere oportuno, ya que, puede ser que el cambio de base de una fracción exacta se convierta en una fracción periódica. La parte fraccionaria del número buscado lo formarán las partes enteras de los números que se hayan ido obteniendo en cada producto, cogidas en ese mismo orden.

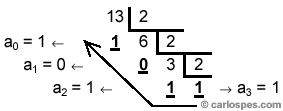
Ejemplo: Para convertir el número 13,3125₁₀ a base 2, en primer lugar hay que dividir, sucesivamente, la parte entera del número, en este caso (13₁₀), entre 2, hasta obtener un cociente más pequeño que 2.

Como el último cociente (a₃), que vale (1), ya es más pequeño que el divisor (2), hay que parar de dividir. Por tanto,

13₁₀ = 1101₂

El segundo paso consiste en convertir la parte fraccionaria del número (0,3125₁₀). Para ello, se deben realizar los siguientes cálculos:

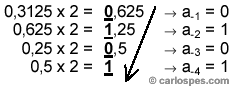La parte fraccionaria desaparece después de realizar cuatro multiplicaciones. Así pues,

0,3125₁₀ = 0,0101₂

En resumen,

13,3125₁₀ = 1101,0101₂

Para comprobar si los cálculos están bien hechos, podemos realizar la conversión inversa, es decir, podemos pasar el número 1101,0101₂ a base 10. De manera que, usando el TFN los cálculos son:

1101,0101₂ = 1∙2³ + 1∙2² + 0∙2¹ + 1∙2⁰ + 0∙2^-1 + 1∙2^-2 + 0∙2^-3 + 1∙2^-4 =

= 8 + 4 + 0 + 1 + 0 + 0,25 + 0 + 0,0625 =

= 13,3125₁₀