En
este sistema de representación, los números
positivos se expresan igual que en Signo
Magnitud o que en Binario
Puro. Sin embargo, para escribir los números
negativos se utiliza el Complemento
a la Base Menos 1. De forma normalizada, el Complemento a la Base Menos 1
de un número entero positivo N de base b, se expresa de la
siguiente manera:
Cb-1(N)
= bn - 1 - N
siendo n el
número de cifras destinadas a representar al
número. Por tanto, en codificación binaria, el Complemento a 1 (C1) de un
número entero positivo (N)
se puede expresar como:
C1(N)
= 2n - 1 - N = NC1
En Complemento a 1, el rango de representación es el mismo
que en Signo Magnitud:
Figura. Rango
de representación en Complemento a 1.
Ejemplo
1: En Complemento a 1, para n = 16, el rango de
representación es:
Así pues, se pueden representar 216 -
1 = 65535 números enteros, que van desde el -3276710
hasta el 3276710.
Ejemplo
2: En Complemento a 1, para n = 16, el
número positivo 950310
se representa igual que en Signo Magnitud o que en Binario Puro:
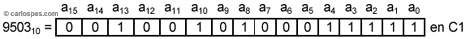Por tanto,
950310
= 0010010100011111C1 = 0010010100011111SM
= 0010010100011111BP
Ejemplo
3: En Complemento a 1, para n = 16, el
número -950310
se escribe calculando el Complemento a la Base Menos 1 del
número 950310
escrito en base 2, es decir, del número 100101000111112:
C1(N)
= C1(10010100011111) =
=
2n - 1 - N =
=
216 - 1 - 10010100011111 =
=
10000000000000000 - 1 - 10010100011111 =
=
1101101011100000C1
En consecuencia,
-950310 =
1101101011100000C1
Obsérvese que, el Complemento a 1 de un número
entero positivo (N)
escrito en binario es el resultado de cambiar todos los bits de valor,
es decir, todos los ceros por unos y todos unos por ceros.
Por otra parte, dado un número entero positivo (N)
en Complemento a 1, para calcular su valor en base 10, se puede
utilizar la misma fórmula que en Signo Magnitud o que en
Binario
Puro.
Un número (N)
representado en Complemento a 1 es positivo si el bit más
significativo es cero. En caso contrario, el número
será
negativo, y para calcular su valor en base 10, habrá que
cambiar
todos los unos por ceros y todos los ceros por unos, obteniendo
así su correspondiente número positivo, al cual
sí
se le puede aplicar una de las fórmulas anteriores y
cambiarle
el signo al resultado.
Ejemplo
4: Si se desea calcular el
valor en base 10 del número 1111101011111101C1,
puesto que el bit más significativo es un 1, sabemos que es
negativo, por tanto, en primer lugar, cambiaremos los ceros por unos y
los unos por ceros:
1111101011111101C1(negativo) →
0000010100000010C1(positivo)
y, en segundo lugar, calcularemos el valor en base 10 del
número
obtenido, con la misma fórmula que se emplea para los
números escritos en Signo Magnitud:
0000010100000010C1
= ( (1 - 2∙0) ∙ (1∙210 + 1∙28
+ 1∙21) )10 =
= ( (1) ∙ (1024 + 256 + 2) )10
= 128210
o con la misma fórmula utilizada para números
representados en Binario Puro:
0000010100000010C1
= ( 1∙210 + 1∙28 + 1∙21
)10 = ( 1024 + 256 + 2 )10
= 128210
De forma que:
1111101011111101C1(negativo)
= -( 0000010100000010C1(positivo) )10
= -128210
es decir,
1111101011111101C1
= -128210
Por otro lado, al igual que ocurría en Signo Magnitud, el
número 010
también tiene dos representaciones en Complemento a 1.
Ejemplo
5: Para n = 16, el
número 010
se puede escribir de dos formas en Complemento a 1:
010 =
0000000000000000C1 = 1111111111111111C1
|
