En este sistema de representación, los números positivos se expresan igual que en Signo Magnitud o que en Binario Puro. Sin embargo, para escribir los números negativos se utiliza el Complemento a la Base. Formalmente, el Complemento a la Base de un número entero positivo N de base b, se expresa de la siguiente manera:

C_b(N) = bⁿ - N

siendo n el número de cifras empleadas en la representación del número. Por tanto, en codificación binaria, el Complemento a 2 (C2) de un número entero positivo (N) se puede expresar como:

C₂(N) = 2ⁿ - N = N_C2

El rango de representación en Complemento a 2 es:

Figura - Rango de representación en Complemento a 2.

Ejemplo 1: En Complemento a 2, para n = 16, el rango de representación es:

Ejemplo de representación en Complemento a 2

Ejemplo 2: En Complemento a 2, para n = 16, el número positivo 9503₁₀ se representa igual que en Complemento a 1, Signo Magnitud o Binario Puro:

9503₁₀ = 0010010100011111_C2 = 0010010100011111_C1 = 0010010100011111_SM = 0010010100011111_BP

Ejemplo 3: En Complemento a 2, para n = 16, el número -9503₁₀ se escribe calculando el Complemento a la Base del número 9503₁₀ representado en base 2, es decir, del número 10010100011111₂:

C₂(N) = C₂(10010100011111) =

= 2ⁿ - N =

= 2¹⁶ - 10010100011111 =

= 10000000000000000 - 10010100011111 =

= 1101101011100000_C2

En consecuencia,

-9503₁₀ = 1101101011100001_C2

Fíjese que, el Complemento a 2 de un número entero positivo (N) escrito en binario es el resultado de cambiar todos los bits de valor (ceros por unos y unos por ceros), obteniendo así el Complemento a 1 del número y, después, sumarle 1.

C₂(N) = C₁(N) + 1 = N_C1 + 1 = N_C2

De esta manera, en tan solo dos pasos se puede calcular, fácilmente, el Complemento a 2. Por ejemplo, dado el número:

para calcular el Complemento a 2, en un primer paso se calcula el Complemento a 1 de dicho número:

y, en un segundo paso, se le suma 1 al número obtenido en Complemento a 1:

El resultado es el esperado:

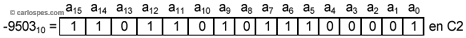Por otro lado, si se pretende calcular el valor en base 10 de un número entero positivo (N) escrito Complemento a 2, se puede usar la misma fórmula que en Signo Magnitud o que en Binario Puro.

Un número (N) representado en Complemento a 2 es positivo si el bit más significativo es cero. En caso contrario, el número será negativo, y para calcular su valor en base 10, se tiene que utilizar la fórmula:

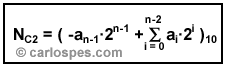Figura - Fórmula para calcular, en base 10, el valor de un número entero negativo escrito en Complemento a 2.

Ejemplo 4: Para calcular el valor en base 10 del número 1001000000000110_C2, se debe emplear la fórmula anterior. De tal forma que:

1001000000000110_C2 = ( (-1∙2¹⁵) + (1∙2¹² + 1∙2² + 1∙2¹) )₁₀ = ( (-32768) + (4102) )₁₀ = -28666₁₀