Con el Sistema de Numeración Arábigo o Decimal se pueden representar infinitos números reales. Para ello, se utilizan diez cifras o dígitos numéricos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 (diez son los dedos de las manos). También se usan los signos más (+) y menos (-) para representar a los números positivos y negativos, respectivamente, y un punto (.) o una coma (,) para separar la parte entera de la parte fraccionaria.

Numero real = parte entera , parte fraccionaria

Ejemplo 1: Los números 5,6 y -502,12 representan a los números "cinco con seis" y "menos quinientos dos coma doce".

5,6 = 5 + 0,6
-502,12 = -500 - 2 - 0,1 - 0,02

Una de las características más importantes del Sistema Decimal es que es un sistema de numeración posicional.

Sistemas de Numeración Posicionales

En un sistema de numeración posicional, cada cifra representa a un valor relativo diferente, dependiendo de su valor absoluto y de su posición en una secuencia de dígitos. Esta característica le convierte en un sistema de numeración adecuado para realizar operaciones matemáticas por escrito, tales como: la suma, la resta, la multiplicación o la división.

Ejemplo 2: En el Sistema Decimal, el número entero "cuatrocientos cuarenta y cuatro" se representa como 444. Empezando por la izquierda, el primer 4 representa al "cuatrocientos" (400), el segundo 4 representa al "cuarenta" (40) y el último 4 representa al "cuatro" (4). En este caso, las tres cifras tienen como valor absoluto: el 4, y como valores relativos: el 400, el 40 y el 4.

444 = 400 + 40 + 4

Un sistema de numeración posicional se caracteriza por su base, que viene determinada por el número de dígitos que utiliza.

Ejemplo 3: La bases de los Sistemas Decimal, Binario, Octal y Hexadecimal son 10, 2, 8 y 16, debido a que usan diez, dos, ocho y dieciséis cifras, respectivamente. En la siguiente tabla se muestran los dígitos de cada uno de estos sistemas de numeración.

Sistemas de numeración en base 2, 8, 10 y 16

Figura. Dígitos de los sitemas de numeración de base 2, 8, 10 y 16.

Los signos hexadecimales A, B, C, D, E y F equivalen, respectivamente, a los números 10, 11, 12, 13, 14 y 15 en base 10.

En cualquier sistema de numeración posicional, una secuencia de dígitos se puede representar, formalmente, de la siguiente manera:

N_b = a_p-1 a_p-2 ... a₁ a₀ , a_-1 a_-2 ... a_-q+1 a_-q

siendo (N) el número o secuencia de signos, (b) la base, (p) el número de dígitos de la parte entera, (q) el número de dígitos de la parte fraccionaria, (a_i) las cifras del número e (i) la posición de cada cifra con respecto a la coma (,). Cumpliéndose que para todo dígito a,

0 <= a <= b-1

y para toda posición i,

-q <= i <= p-1

Ejemplo 4: En el Sistema Decimal, el número real 4305,86 se puede expresar como

4305,86₁₀

siendo el número N = 4305,86, la base b = 10, el número de dígitos de la parte entera p = 4, el número de dígitos de la parte fraccionaria q = 2 y las cifras a₃ = 4, a₂ = 3, a₁ = 0, a₀ = 5, a_-1 = 8 y a_-2 = 6. Cumpliéndose que para todo dígito a,

0 <= a <= 9

y para toda posición i,

-2 <= i <= 3

Ejemplo 5: En el Sistema Binario, el número 11010,001 se puede enunciar como

11010,001₂

siendo el número N = 11010,001, la base b = 2, el número de dígitos de la parte entera p = 5, el número de dígitos de la parte fraccionaria q = 3 y las cifras a₄ = 1, a₃ = 1, a₂ = 0, a₁ = 1, a₀ = 0, a_-1 = 0, a_-2 = 0 y a_-3 = 1. Cumpliéndose que para todo dígito a,

0 <= a <= 1

y para toda posición i,

-3 <= i <= 4

Otra característica importante de los sistemas de numeración posicional es que con n dígitos se pueden representar bⁿ números diferentes.

Ejemplo 6: Con tres dígitos, en el Sistema Decimal se pueden representar 10³ números enteros positivos distintos, es decir, mil números: del 000₁₀ al 999₁₀, ambos inclusive.

Ejemplo 7: Con tres dígitos, en los Sistemas Binario, Octal y Hexadecimal se pueden representar 2³, 8³ y 16³ números distintos, respectivamente, es decir, 8, 512 y 4096 números, que van desde el 000₂ hasta el 111₂, desde el 000₈ hasta el 777₈ y desde el 000₁₆ hasta el FFF₁₆.

Teorema Fundamental de la Numeración

El Teorema Fundamental de la Numeración (TFN) establece que en cualquier sistema de numeración posicional, todos los números pueden expresarse mediante la siguiente suma de productos:

N_b = a_p-1·b^p-1 + a_p-2·b^p-2 + ... + a₁·b¹ + a₀·b⁰ + a_-1·b^-1 + a_-2·b^-2 + ... + a_-q+1·b^-q+1 + a_-q·b^-q

es decir,

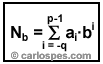Figura - Fórmula del Teorema Fundamental de la Numeración.

Ejemplo 8: Aplicando el TFN, el número real 4305,86, en base 10, se puede expresar como:

4305,86₁₀ = 4∙10³ + 3∙10² + 0∙10¹ + 5∙10⁰ + 8∙10^-1 + 6∙10^-2

4305,86₁₀ = 4∙1000 + 3∙100 + 0∙10 + 5∙1 + 8∙0,1 + 6∙0,01

4305,86₁₀ = 4000 + 300 + 0 + 5 + 0,8 + 0,06

En la secuencia de dígitos a_p-1 a_p-2 ... a₁ a₀ , a_-1 a_-2 ... a_-q+1 a_-q cada cifra tiene un peso diferente a las demás. El peso de un dígito viene determinado por su posición respecto a la coma (,) decimal. Cuanto más a la izquierda se encuentra un dígito, más peso tiene, es decir, más significativo es. Por tanto, el dígito más significativo o de mayor peso es a_p-1 y el menos significativo o de menor peso es a_-q. Esto es así porque el peso de a_p-1 es b^p-1 y el peso de a_-q es b^-q.

Ejemplo 9: En la secuencia de dígitos 4305,86, en base 10, el signo más significativo es el 4, que representa al 4000, ya que su peso es 10³, y el menos significativo es el 6, que representa al 0,06, ya que su peso es 10^-2.

En resumen, el TFN dice que en cualquier sistema de numeración posicional de base b, un número N representa a la suma acumulada de los productos de sus dígitos a_p-1, a_p-2, ..., a₁, a₀, a_-1, a_-2, ..., a_-q+1 y a_-q por sus respectivos pesos b^p-1, b^p-2, ..., b¹, b⁰, b^-1, b^-2, ..., b^-q+1 y b^-q.