En
la representación de un número entero en Signo Magnitud,
también llamada Signo
Módulo, de los n bits
participantes en dicha representación, el más
significativo se encarga de representar al signo del mismo,
denominándosele bit
de signo. El resto de bits representan a la magnitud. Por
tanto, dado un número en Signo Magnitud de n bits,
NSM
= an-1 an-2 ... a1
a0
el bit an-1
representa al signo del número y el resto de bits: an-2,
..., a1
y a0,
a la magnitud del mismo.
Cuando se quiera representar a un número negativo, el bit de
signo valdrá 1,
siendo 0
cuando el número sea positivo. El rango de
representación de este sistema es el siguiente:
Figura.
Rango de representación en Signo Magnitud.
Ejemplo
1:
En Signo Magnitud, para n
= 8, el bit a7 representa al signo
del número, y el resto de bits: a6, a5, a4, a3, a2, a1 y a0,
a la magnitud del mismo:
Su rango de representación es:
Por consiguiente, se pueden representar 28 - 1 =
255 números enteros, que van desde el -12710
hasta el 12710.
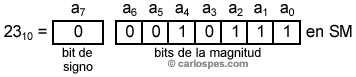
Ejemplo
2: En Signo Magnitud,
para n = 8,
el número 2310 se escribe:
Al ser un número positivo, el bit de signo vale cero (a7 = 0)
y, como se puede observar, los números positivos escritos en
Signo Magnitud se representan igual que si se escribiesen en Binario
Puro:
2310 =
00010111SM = 00010111BP
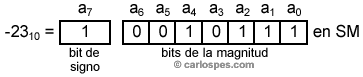
Ejemplo
3: En Signo Magnitud, para n = 8, el
número -2310
se simboliza con la misma magnitud que el número 2310,
diferenciándose, solamente, en el bit de signo, que al
tratarse de un número negativo, ahora tiene que valer 1, en vez de 0. Así
pues, su representación es:
Por tanto,
-2310
= 10010111SM
Por otro lado, para calcular el valor en base 10 de un
número entero (N)
escrito en Signo Magnitud, hay que hacer uso de la fórmula:
Figura. Fórmula
para calcular, en base 10, el valor de un número entero
escrito en Signo Magnitud.
Ejemplo
4: Para calcular los valores en
base 10 de los números 11100001SM
y 00011010SM,
se debe emplear la fórmula anterior. De tal manera que:
11100001SM
= ( (1 - 2∙1) ∙ (1∙26 + 1∙25
+ 1∙20) )10 =
=
( (1 - 2) ∙ (64 + 32 + 1) )10 = ( (-1) ∙ (97) )10
= -9710
00011010SM
= ( (1 - 2∙0) ∙ (1∙24 + 1∙23
+ 1∙21) )10 =
=
( (1 - 0) ∙ (16 + 8 + 2) )10 = ( (1) ∙ (26) )10
= 2610
Obsérvese que, en Signo Magnitud, al problema de
desbordamiento se le suma que el número 010
tiene dos representaciones.
Ejemplo
5: En Signo Magnitud, para n = 8, el
número 010
se puede escribir de dos formas:
010 =
00000000SM = 10000000SM
|
